What is FM Synthesis (Frequency Modulation Synthesis)?
- Tunç Çakır

- Aug 21, 2022
- 6 min read
Updated: Jul 16, 2025

Subtractive synthesis is generally more widespread, known, and utilized compared to FM synthesis. However, FM synthesis operates on the opposite logic, allowing for the easy creation of rich, complex waveforms and quick shaping of simple waveforms through a more additive approach. It has become an important part of contemporary electronic music, but delving into this topic without establishing fundamental principles from the outset can be somewhat complex and challenging. Now, let's take a look at the fundamental elements of FM theory.
FM is an abbreviation. It stands for Frequency Modulation. When we remove all the harmonics in a waveform, what remains is a sine wave at the fundamental frequency. These harmonics are exactly what creates the tonal differences between a piano and a guitar playing the same melody. When both instruments play the same melody, we can easily distinguish between a piano and a guitar even with our eyes closed. This is because the harmonics in the two instruments are present in very different ways.
In FM synthesis, although many different waveforms can be used, it is fundamentally created by combining two sine waveforms. One important point here is that this combining process is not like summing in a mixer. If there are two oscillators (OSC) in FM synthesis, one modulates the frequency of the other. The oscillator we hear is called the "Carrier," while the one performing the modulation is called the "Modulator." Another important aspect for music is that the frequencies for FM modulation must be within the range of human hearing, between 20Hz and 20kHz.
Oscillators and what we call LFOs (Low-Frequency Oscillators) are essentially the same things. They perform the same functions and generate frequencies and waveforms in the same way. However, in FM synthesis, if the modulating OSC falls below 20Hz, it is no longer perceived as a frequency by our ears, and the effect it has on the other oscillator is not considered FM synthesis. Instead, it produces an LFO modulation, like a vibrato effect. For FM synthesis to occur, both the oscillator we hear and the modulating oscillator need to be between 20Hz and 20kHz. As a result, a completely new frequency range and a new waveform will be created.
So, to change the waveform and spectrum, we do not necessarily need a resonant filter. There are many other ways to achieve this. Fundamentally, there are three types of FM: Exponential FM, Linear FM, and Through Zero (Thru Zero or TZ) FM.

FM synthesis, by the mid-20th century, was seen as a means of transmitting sound and was used for radio broadcasting. Therefore, it utilized high frequencies well above the human hearing range. John Chowning, whose work began at Stanford University in California in the 1960s, made the greatest contribution to FM synthesis. FM was officially discovered around 1967 and began to take its final form. The definition of "Algorithm" in FM synthesis was licensed by Yamaha in 1973. This commercialized application by Yamaha closely resembles Phase Distortion synthesis, with results that are mathematically almost 90% identical. John Chowning primarily developed digital FM synthesis, after which FM synthesis took its final shape.
In 1974, Yamaha produced its first digital synthesizer prototype. In 1978, New England Digital implemented a design with a patent obtained from Yamaha for the Synclavier. In 1981, Yamaha introduced the GS-1 design. Yamaha's DX7, released in 1983, is renowned as the first successful digital synthesizer. Yamaha, having secured the FM synthesis patent, further developed Phase Distortion approaches in the Casio CZ series.
In analog systems and synthesizers, Don Buchla pioneered the application of FM and AM techniques in the 1960s. This approach later became common in Moog and ARP synthesizers. FM synthesis, following the advancements by John Chowning and Yamaha, was recognized as a synthesis technique in the digital world for about 20 years. Analog systems had a different scenario; in FM synthesis, the carrier oscillators experienced "tune drift." While Exponential FM and Linear FM techniques were developed in the analog domain, Through Zero FM was discovered and implemented in the digital realm. In analog, adjusting oscillators might be necessary when performing FM, or options in more atonal ranges could be explored. In analog, the 1V/oct input serves the same function as Exponential FM input; both result in Exponential FM when FM is applied. For Through Zero FM or Linear FM, separate inputs need to be designed, and the signal must be directed to these inputs. Linear FM inputs are always AC coupled, whereas Through Zero FM inputs can be both AC and DC coupled. Hence, AC coupled inputs do not accept low frequencies or DC signals operating solely in the positive range. Through Zero FM can modulate without altering the fundamental frequency of the carrier oscillator (without tune drift) and can add harmonics. Achieving and coding Through Zero FM in digital environments is easier compared to programming Exponential FM, which requires greater effort digitally. Conversely, in analog, Exponential FM is naturally present, while the Through Zero concept remained undiscovered in the analog world for many years.
At VAEMI, we developed a Through Zero FM design for the analog world that applies the same mathematics as waveforms achieved through digital Through Zero FM or Phase Distortion Synthesis. Despite few companies implementing this approach worldwide, our design stands out with unmatched sound quality, utilizing waveshaper methods and high-quality Through Hole components.



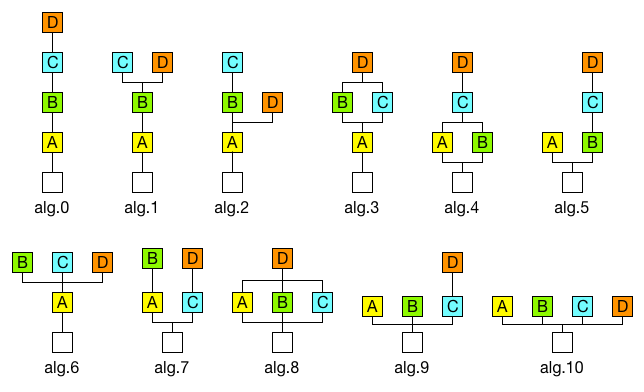
n FM synthesis, all oscillators are referred to as 'operators.' There is a carrier operator, which is essentially the oscillator we primarily listen to. The other operators are called 'modulators.' While these modulator operators can be audible, they are generally used to modulate the carrier operator or other modulator and carrier operators for modulation purposes. In FM synthesis, you can use 2, 3, 4, 6, 8, 10, 12, or even more operators. These operators can be connected in series or parallel and directed towards the carrier operator. These routings are referred to as 'algorithms.' In a synthesizer with 4 operators, there can be approximately 10 or more algorithms.

Let's now take a look at the structure of the operator. Briefly, there is an audio signal chain in the form of Input ► Oscillator ► Amplifier ► Output. There is an envelope generator that controls the amplifier. The keyboard controls the oscillator's frequency and triggers the envelope generator. The envelope generator connected to the amplifier allows you to shape the FM tone (similar to the classic filter envelope).
If you are setting up an analog monophonic synth voice structure, you will need to trigger many envelopes simultaneously and be able to control the tuning of oscillators at the same time.

When creating waveforms, in the context of Through Zero FM, frequencies that are the same as or multiples of the fundamental frequency are used. When used in this way, you can employ FM modulation more musically without losing the fundamental frequency. Frequencies outside of these or detuning operator adjustments are optional and can be used.
Musically tuned frequencies can also be expressed as follows: When you adjust the harmonics of the fundamental frequency sequentially, you can create FM modulations that are musical and retain the fundamental frequency. Even though we primarily use sine waves, by mixing sine waves and applying FM modulation, you can easily achieve waveforms like saw waves or square waves.Square wave gibi wave formlara da rahatlıkla ulaşabilirsiniz.
In conclusion, if we need to discuss some important points and tips, it's generally advisable to choose smooth waveforms when working with FM synthesis, such as sine waves. Triangle waves also produce pleasing tones. Other waveforms, especially saw or square waves, can sometimes produce harsh and sharp sounds that are more challenging to control. However, it's not impossible to work with these waveforms; you can use them to achieve very different and interesting results. There's also the option to create feedback within one operator to conduct FM synthesis, which allows you to obtain a spectrum ranging from a sine wave to a saw wave and progress in that area. Experiment with all the algorithms and try to understand the colors each one produces. Over time, you'll develop a sense for it. FM synthesis allows you to capture a unique tone because the possibilities are truly extensive. This approach differs significantly from synthesizing with just basic waveforms. By using this approach, you can create various acoustic tones like synth bass, piano, bells, chimes, wind instruments, drums, sound effects, or even explore more surreal concepts.




Comments